快慢指针找环起点
Given a linked list, return the node where the cycle begins. If there is no cycle, return null. There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter. Notice that you should not modify the linked list. 142. Linked List Cycle II
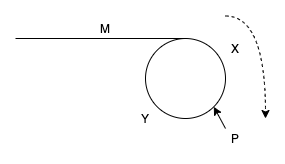
很简单的一道题,很久没看都快忘记了。
推理过程
因为快指针的速度是慢指针的两倍,所以快指针的走过的距离为慢指针的两倍
\[S_{fast} = 2 * S_{slow}\]快指针和慢指针在P点相遇,距离公式展开为:
\[M + N * (Y + Y) + X = 2 * (M + X)\]这里慢指针不可能绕环一圈而不与快指针相遇(当慢指针进入环时,它与快指针的距离肯定是小于环的长度的,如果慢指针走了一圈,那么快指针肯定走了两圈,其肯定相遇。有没有可能恰好错过呢?不能。譬如慢指针与快指针相差1,则会在下一次相遇,若相差2,则会在下两次相遇)。
所以这里的慢指针距离为2 * (M + X),依次展开为:
\[N * (Y + Y) = M\] \[(N - 1) * (X + Y) + (X + Y) = M + X\] \[(N - 1) * (X + Y) + Y = M\]去掉环得到:
\[Y = M\]代码就是先找到相遇点,再让其同时出发,再次相遇即为环起始点:
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null || head.next == null) {
return null;
}
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
break;
}
}
if (fast == null || fast.next == null) {
return null;
}
slow = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}